The Linear Algebra Kernel is an essential piece in the engineer’s and scientist’s tool box, there are many implementations both specific implementations for special usage and more generic implementations which remain efficient.

Advent of GPU architecture has opened up new horizons and some new linear algebra kernels have emerged. In the ANALYST project a Laplace problem has been optimized in several ways and several kernels have been benchmarked. In particular the well known Intel MKL  library is compared to two OpenCL linear algebra implementation. The first using the ViennaCL  library and the second using a from scratch implementation.

RLGC matrices of a cable harness depend on its cable arrangement cross-section [5]. To compute these matrices, it is needed to solve the Poisson’s equation in the plane with Dirichlet’s boundary conditions in accordance with the contours of the section conductors.

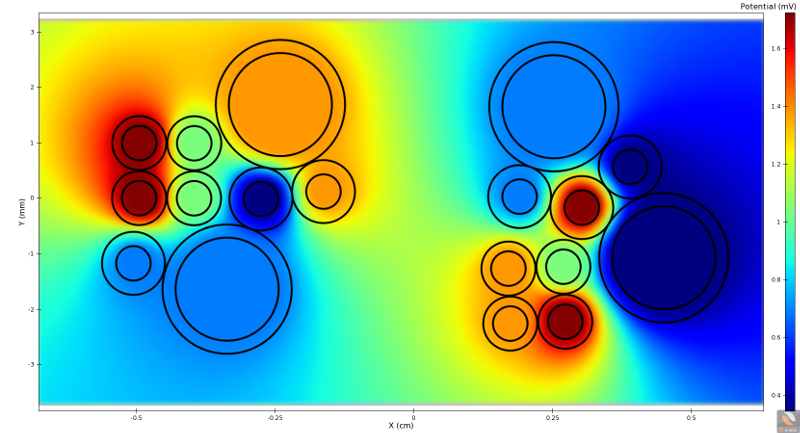
The potential V allows computing the charge on a conductor by integrating the normal derivative of V.

A set of specific boundary conditions is chosen to compute the capacitance matrix and the inductance matrix by setting the potential to be equal to 1 on one of the conductors and 0 on the others.

The following figure shows the potential on a section made of 18 insulated conductors. Each conductor has been put to an arbitrary-chosen potential. The potential is represented on a uniform grid enclosing the conductors.

We use these linear algebra kernels on several hosts. The following table gives the specification of these hosts.

Here is the computation time in seconds of several sections containing up to 700 conductors.

The internal linear solver and the ViennaCL solver have been used with a NVIDIA GeForce GTX 1660 Ti GPU. The MKL is used with an AMD Ryzen 7 2700 CPU.

On this platform, the Intel MKL is the linear algebra for small configurations.

For intermediate configurations ViennaCL and Intel MKL are competitive. The from scratch Gauss elimination implementations are generally the least efficient.

Finally, for huge configurations, the GPU implementation is limited by the maximal size of a buffer. The case containing 700 conductors can only be executed on the CPU with the Intel MKL.

We can also examine the worst and best computation times for each test case across all hosts.

The following table presents these times in seconds. These results confirm the previous conclusion even if they nuance them a little.

The next figures represent these times and the speed up regarding the best time we could achieve before optimization developed during the ANALYST project. We can see that, even if we consider the best results as a reference time, we can now compute the RLCG matrices always with a positive gain. The best time of computation is obtained with MKL kernels with a speedup up to 6.

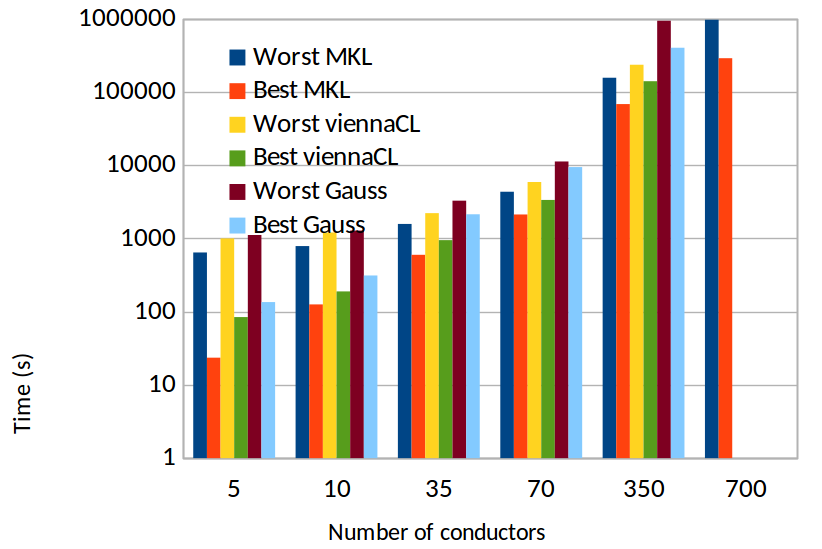
Fig. 2 – Best and worst times of the computation of the RLCG matrices with the different linear algebra kernels depending on the number of conductors. The y-axis is represented as a log scale.

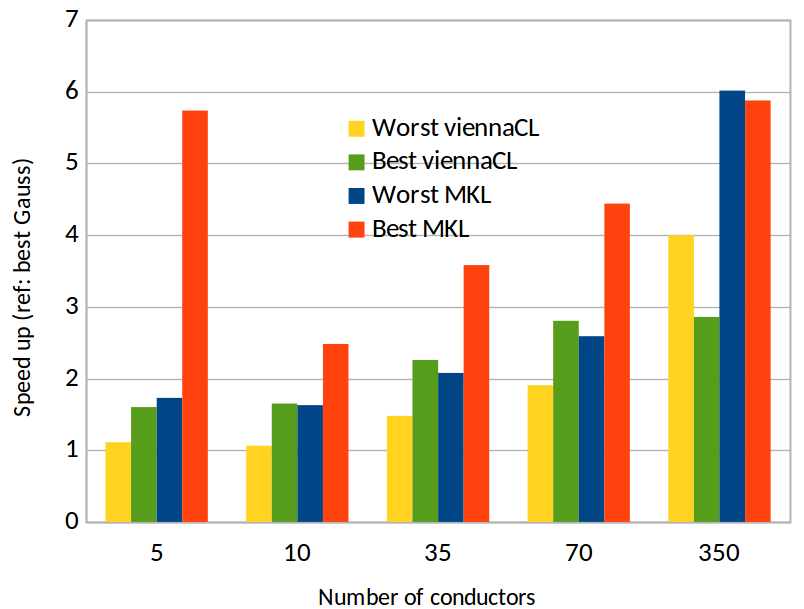
Fig. 3 – Speed up of the computation of the RLCG matrices with the different linear algebra kernels depending on the number of conductors. The reference times are the best and worst times of computation using the Gauss-elimination kernel, that is the best and worst times we could achieve at the beginning of the Analyst project.

We can also examine which machine provides the best and worst times of computation.

We can see the size of the problem changes according to which machine has the best performances. In particular, the available RAM on the GPU has an important impact. In small cases (up to 70 conductors), the GPU with smaller RAM has the best performances, but with larger cases, the GPU with larger RAM has the best performances.

For the CPU, the recent Intel CPU has the best performances, because the Intel MKL is developed by Intel and benefits from a higher level of optimization on this kind of CPU.

These times of computation have been obtained on workstations and machines dedicated to computation. On a laptop, the tendency is somehow similar, but in larger cases, the ViennaCL kernel achieves better performances.

Finally, this shows that the MKL is the best alternative in most cases, except when the CPU has a low number of cores. In this case, using the ViennaCL library allows achieving good performance.

The performance of linear algebra kernel implementation is strongly impacted by the host architecture (CPU architecture, type of RAM, GPU memory and GPU generation). Therefore there is no major tendency to identify the best kernel implementation. A dynamic strategy has finally been chosen to pick the best kernel at run time. This way we have a speedup from 2 up to 6 for a representative host architecture sample.

Despite the fact that there is no big trend, we note that the CPU libraries remain very competitive for this type of problems especially for small issues (not waiting) and for important difficulties (memory limit of GPUs).

This project has received funding from the Clean Sky 2 Joint Undertaking of the European Union’s Horizon 2020 research and innovation program under grant agreement No 821128.