Tilted mesh

The tilted mesh specification aims at generalizing the structured mesh description to oblique oriented faces. Surfaces and volume faces are again defined by hexaedral’s nodes by are not limited to axis aligned nodes. The following section gives the rules to creating objects made of predefined faces and volumes.

A tilted mesh is a named HDF5 group child of /mesh having an attribute type equals tilted.

A structured mesh is composed of three children :

• A mandatory child :

  • a cartesianGrid group

• Two optional children :

  • a group HDF5 group

  • a groupGroup HDF5 group

Cartesian grid

The tilted mesh’s cartesian grid definition is exactly the same as for the structured mesh. The reader can refer to Cartesian grid for more details.

As an example, in dimension 3, the cartesian grid is defined by 3 children floatingType called x, y and z :

data.h5
`-- mesh/
    `-- $gmesh1
        `-- $structured-mesh-3d[@type=tilted]/
            `-- cartesianGrid
                |-- x[@physicalNature=length
                |     @unit=meter]
                |-- y[@physicalNature=length
                |     @unit=meter]
                `-- z[@physicalNature=length
                      @unit=meter]

The physical nature of x, y and z is length and the unit is meter.

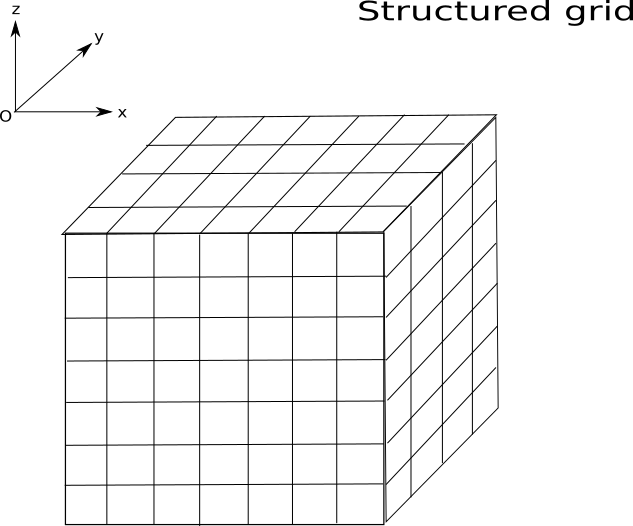
A structured orthogonal grid

Element node numbering

The corners of hexaedral elements of the structured grid are uniquely numbering. This numbering is used in the definition of faces and volumes.

The following figure shows a structured element and the numbering convention:

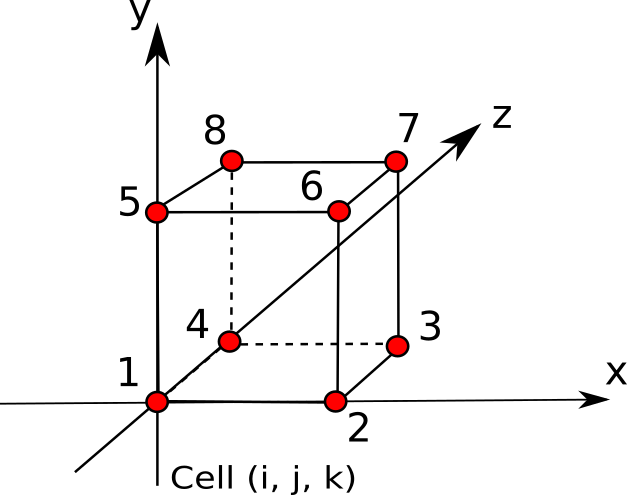
The numbering convention for a structured element

Element

A tilted element is defined by:

• The min max indices of the structured element carrying the tilted element : (imin, jmin, kmin, jmax, kmax, kmax)

• A type : a predefined integer which represents the nodes used in the element definition

• A normal defined in the same way the normal is defined for a structured mesh face

As said above, elements definition is based upon predefined elements identified by a type, a support and a node list.

The predefined element table is given hereafter:

Type	Support	Nodes
0	face	1, 2, 3, 4
1	face	1, 2, 4
2	face	1, 2, 3
3	face	2, 3, 4
4	face	1, 3, 4
5	volume	2, 4, 5
6	volume	1, 6, 3
7	volume	2, 7, 4
8	volume	1, 3, 8
9	volume	1, 8, 6
10	volume	2, 5, 7
11	volume	3, 6, 8
12	volume	4, 5, 7
13	volume	1, 2, 7, 8
14	volume	2, 3, 8, 5
15	volume	3, 4, 5, 6
16	volume	1, 6, 7, 4
17	volume	1, 5, 7, 3
18	volume	2, 4, 8, 6

Element group

An element group of a tilted mesh is an HDF5 two dimensional dataset children of /mesh/$gmesh/$mesh.

An element group has an HDF5 attribute type, its value is element, in addition, it has an entityType attribute. The entityType attribute is a hdf5 string attribute and gives the type of entities store in the group. entityType can take the following values:

• face : the group contains only surface elements.

• volume : the group contains only volume elements.

The first dimension is the rows. Each row defines 7 integers representing:

• The lowest corner of a parallelepiped

• The highest corner of the same parallelepiped

• The seventh gives the type of the element

Normal

As for structured mesh, normal faces are contained in the /mesh/$gmesh/$mesh/normal group in datasets named as the initial face group in /mesh/$gmesh/$mesh/group.

The possible values of the /mesh/$gmesh/$mesh/normal dataset are:

• For type 0 element, the normal definition is as in the structure mesh specification

• For a tilted element, the normal is defined by the order of the nodes in the type table following the pigtail rule. A sign + or - permits to give the direction of the normal.

Example :

data.h5
`-- mesh/
    `-- $gmesh1/
        `-- $tilted-mesh[@type=tilted]/
            |-- cartesianGrid/
            |-- group/
            |   `- $a_tilted_group[@type=element,
            |                      @entityType=face]
            |       | 0 1 2 1 2 2 0
            |       | 1 1 2 2 2 2 4
            `-- normal/
                `-- $a_tilted_group
                    | +z
                    | +u

groupGroup

groupGroup is an HDF5 group and contains sets of group children. groupGroup children are named HDF5 string dataset, each groupGroup is a set group’s names.

groupGroup definition is the same as the structured mesh groupGroup definition.